For this project, we worked with manipulating faces. One way we did this is by creating a morph from one face to another, and we also created caricatures of faces by comparing them to the average face.
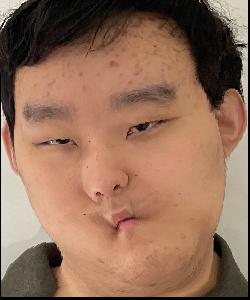
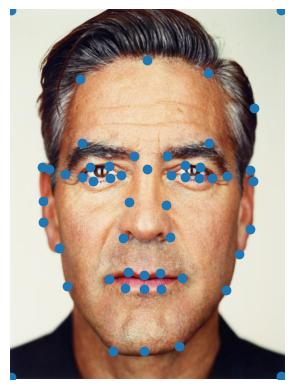
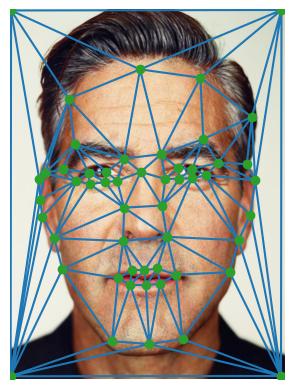
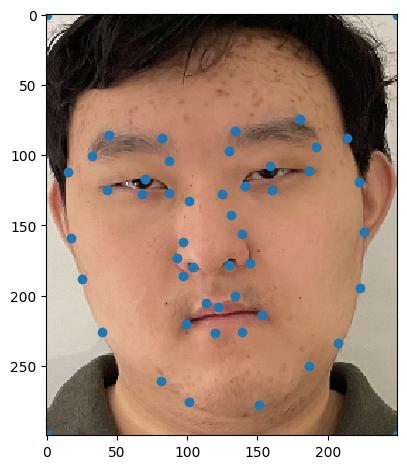
First, we mark corresponding points between two images. I chose myself and the example George photo that was provided. Then, we compute the Delaunay triangulation for these points, as well as the Delaunay triangulation for the average points between the two photos. We also used the labeling tool provided.





In order to compute the mid way face, for each image we compute the transform from its points to the mid-way points (calculated as (points1 + points2) / 2). We compute the affine transformation matrix by taking the dot product of the source matrix and the inverse of the destination matrix. Then, we compute the points in each triangle and warp them from the two original images and average them in the new image. We don't use interpolation as simply rounding provides good results and thus deemed interpolation as unneccesary.


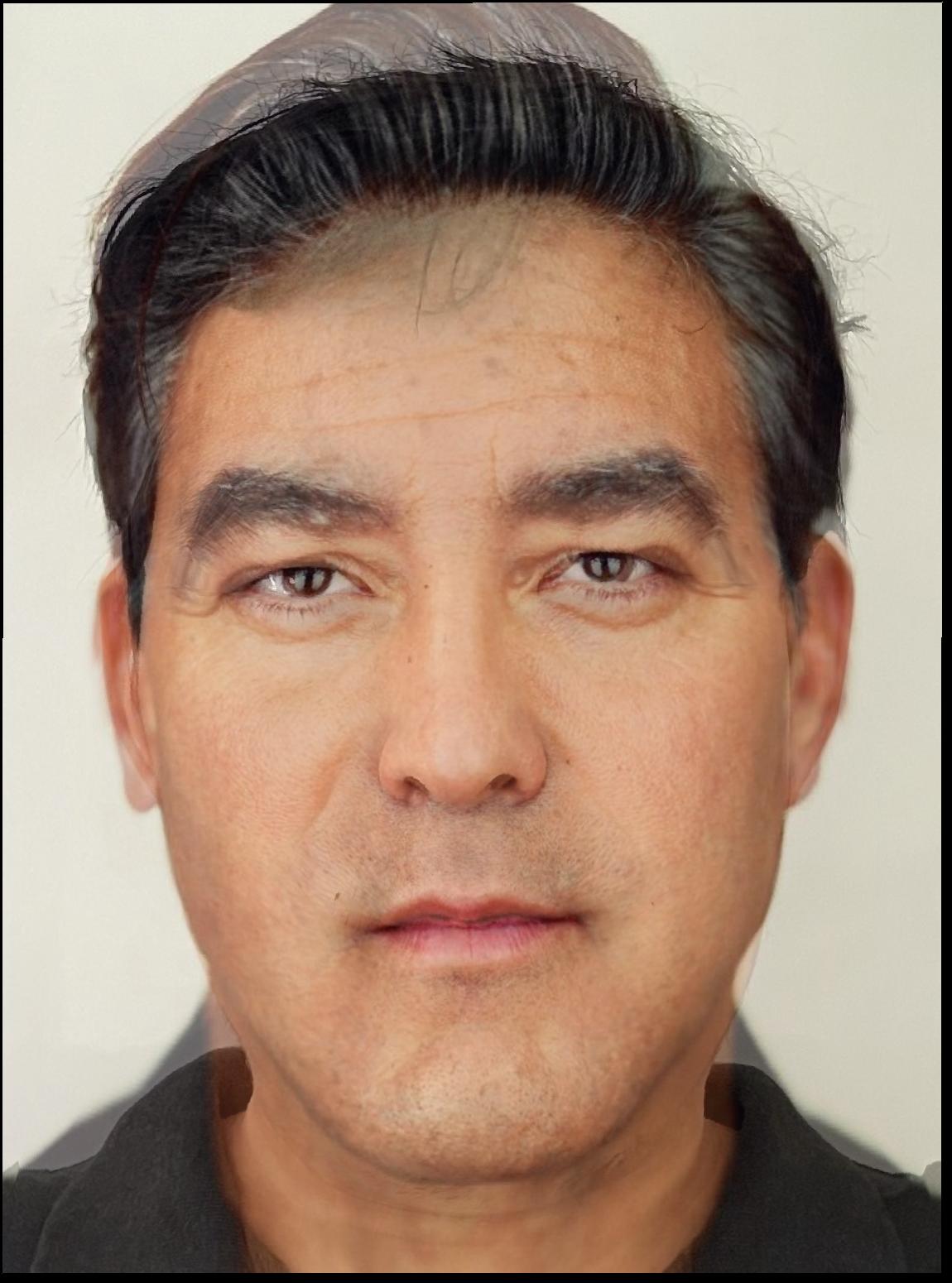
This runs on a similar principle to before, but instead of using a simple averaging for the points and pixel values, we take the weighted average depending on the warp_frac (for the average points) and the dissolve_frac (for the average color), and computing as val2 * frac + val1 * (1 - frac), where 0 is the original image and 1 is the new image. The rest follows the same principle, we compute the affine between the two images and the weighted average of points, and then we take the weighted average of the warped triangles to give us the moprhed image. We do this for 60 frames, varying from 0-1.

We used the FEI face database for these next sections. In this dataset we get a spatially normalized dataset of faces, and corresponding points to these faces.
This dataset also provides both resting and smiling faces. In order to compute the "mean face" of a population, we effectively utilize part 2, but instead of just two faces,
we average multiple (in this case 100) faces. We do this by taking the average points of all the images to get the mean face shape. Then we morph every face into this
average face shape, and then average these images together.
We also warp our face onto the shape of the average face, as well as the average face onto the shape of our face. Due to the difference in the way the photos were taken they
look a little funny but it's nonetheless quite interesting to see. We also reuse the same labeling tool provided in order to generate the correspondences in the same way that
they were done in the FEI dataset.








In order to compute the "caricature", we take the difference between the points of one image and the points of the average image. This essentially gives us what makes us different. We then add this difference onto the original points to exaggerate the difference. We control the amount we want to exaggerate by with a parameter alpha which we control, and multiply the amount of difference we add to the original. In the examples below we choose alpha values of 0.1, 0.25, 0.5, and 1.




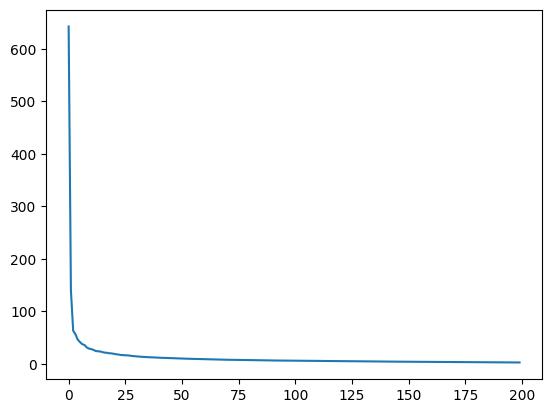
First, we compute PCA on the faces themselves. For this, we compute the singular value decomposition on all the faces, which gives us
U, S, V, where U is the new space for each face, S is the weight of each "eigenface", and V is the original images expressed in the new face space.
We can display these eigenfaces to get an idea behind how PCA works.
Then, we do SVD on the shapes instead of the faces themselves. This time we include the shape of my face as well as the shape of the average face.
This allows us to make caricatures in this new shape basis. In order to do this, we take the difference between the V vectors representing one face
and the average face. We also only take the top few features, 15 in our case. Similar to part 5, we then add some amount of this difference to the
original V vector for the image. Then we reconstruct the resulting shape by computing the dot product between U, S, and the resulting vector, morph a face
into this resulting shape. We use alpha values of 0.25, 0.5, and 1 for this section.